La matematica ci aiuta? / Come misurare la diseguaglianza dei redditi
In un tempo passato, a un viaggiatore in terre lontane capitò di visitare Anastasia e Zobeide. Anastasia era una città bagnata da canali concentrici e sorvolata da aquiloni; una città ingannatrice che appariva come un tutto in cui nessun desiderio andava perduto e di cui ognuno faceva parte, ma in cui non restava che abitare questo desiderio ed esserne contento. Di là, dopo sei giorni e sette notti, si arrivava a Zobeide, città bianca, ben esposta alla luna, con vie che giravano su stesse come in un gomitolo, fondata aspettando di ricreare un inseguimento sognato, senza che quello si ripetesse né nel sonno né da svegli. Il viaggiatore, acuto osservatore, notò che in tutte e due le città gli abitanti si suddividevano in cinque classi, distinte l’una dall’altra per la professione dei loro componenti, ma altrimenti assai omogenee, tra loro e al loro interno. A ciascuna classe si associava non una posizione diversa nell’ordinamento sociale, ma una differenza nel livello di reddito e, quindi, nel tenore di vita. Il viaggiatore registrò questi redditi in una tabella, esprimendoli tutti in ducati, la moneta del suo paese, e correggendoli per annullare le differenze nel costo della vita tra le due città.
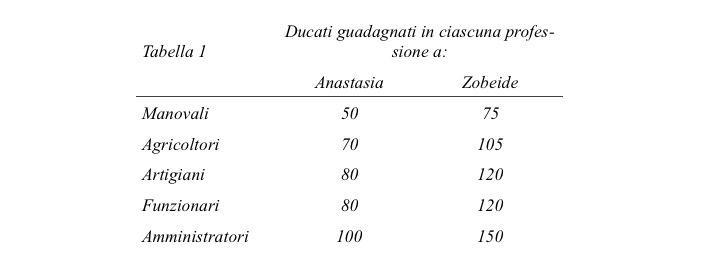
Tornato in patria, una sera mostrò la tabella ad alcuni suoi conoscenti e gli sottopose il seguente quesito “Secondo voi, cari amici, in quale delle due città la distribuzione dei guadagni è più diseguale?”. Il primo a rispondere fu il contabile: “Mi pare che non vi siano dubbi: sono entrambe diseguali in pari misura. Nell’una e nell’altra il reddito dei più ricchi è doppio di quello dei più poveri. Anzi, a ben vedere, per ciascuna classe i redditi a Zobeide sono semplicemente una volta e mezzo quelli ad Anastasia; in tutte e due le proporzioni tra le professioni sono le medesime”. “Credo che ti sbagli”, obiettò il medico: “Non vedi che ad Anastasia gli amministratori hanno 50 ducati più dei manovali, mentre a Zobeide ne hanno 75? Zobeide è certamente più disuguale di Anastasia!”. Intervenne infine il calzolaio, sin allora rimasto in silenzio: “Mah, sarà anche giusto quello che dite, ma se mi fosse chiesto in quale delle due vorrei trasferirmi, senza sapere a quale classe apparterrò, certo sceglierei Zobeide: lì sono tutti più ricchi e, se anche per sventura dovessi ritrovarmi a fare il manovale, vi guadagnerei molti più ducati che ad Anastasia”. La conversazione durò ancora un po’, si arricchì di nuove considerazioni, ma le posizioni non mutarono. Il viaggiatore rifletté che, lungi dal chiarirsi, la questione si era assai ingarbugliata: non avrebbe saputo dire quale fosse la risposta più convincente al suo quesito. Decise che meritava un approfondimento.
Oltre che osservatore acuto, il viaggiatore era uomo di solidi studi. Una rapida ricerca lo portò a individuare vari indici di disuguaglianza. Tra questi rientravano la varianza σ2=Σi(yi–μ)2/n e il coefficiente di variazione c=σ/μ, che gli erano noti sin dal corso di rudimenti di statistica (yi è il reddito dell’individuo i, μ il reddito medio e n il numero totale di individui). Scoprì che la misura più popolare “a livello mondiale” era tuttavia l’indice di concentrazione G proposto da Corrado Gini, un illustre accademico italiano, basato sul confronto a due a due dei redditi di tutti coloro che compongono una comunità: G=ΣiΣj|yi–yj|/2n2μ. Per redditi non negativi, G varia tra 0 nella situazione di perfetta uguaglianza e (n–1)/n in quella di massima disuguaglianza, dove si definisce “perfetta uguaglianza” la situazione in cui tutti hanno lo stesso reddito e “massima disuguaglianza” quella in cui tutto il reddito è concentrato nelle mani di una sola persona. Il viaggiatore trovò anche che gli economisti del lavoro preferivano invece la varianza dei logaritmi VL=Σi[ln(yi)–μln]2/n (μln è la media aritmetica dei logaritmi dei redditi), sia perché VL è un indice “naturale” nelle analisi econometriche in cui le variabili sono espresse in logaritmi sia perché i logaritmi delle retribuzioni tendono a distribuirsi all’incirca normalmente, così che la distribuzione delle retribuzioni può approssimarsi con una specificazione lognormale. Il viaggiatore annotò infine l’idea di un econometrico olandese, Henri Theil, secondo cui misurare l’entropia della distribuzione dei redditi equivale a stimarne il grado di uguaglianza. Partendo dai risultati della teoria dell’informazione, Theil derivava due misure: la deviazione logaritmica media, L=–Σiln(yi/μ)/n, e l’indice che da lui prese poi il nome, T=Σi(yi/μ)ln(yi/μ)/n. Questi due indici hanno la proprietà di essere perfettamente scomponibili per gruppi omogenei di popolazione così che la disuguaglianza totale è la somma esatta, senza alcun residuo, della somma ponderata della disuguaglianza all’interno dei gruppi e della disuguaglianza tra i gruppi. Si è successivamente mostrato come questi due indici appartengano alla famiglia delle misure generalizzate di entropia, che condividono la medesima proprietà di essere additivamente scomponibili. Questa classe di misure è definita da Eβ=[Σi(yi/μ)β/n–1](β2–β)–1, dove β è un parametro da fissare compreso tra –∞ e ∞, che genera la deviazione logaritmica media quando è uguale a 0, l’indice di Theil quando è uguale a 1 e la metà del coefficiente di variazione quando è uguale a 2. Gli indici di questa classe sono compresi tra 0 (perfetta uguaglianza) e ∞ (massima disuguaglianza), tranne la metà del quadrato del coefficiente di variazione e l’indice di Theil i cui limiti superiori sono, rispettivamente, (n–1)/2 e ln(n).
Soddisfatto per l’esito della sua ricerca, il viaggiatore calcolò questi indici per i redditi di Anastasia e Zobeide e li riportò in una nuova tabella.
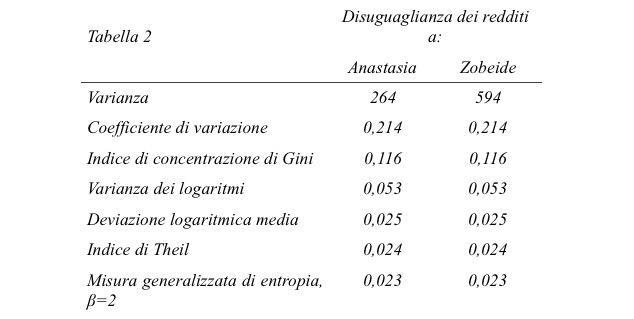
I valori calcolati erano molto diversi tra i vari indici, ma per ciascuno di essi erano uguali in entrambe le città, tranne che nel caso della varianza. Sembra quindi che avesse ragione il contabile: Anastasia e Zobeide avevano lo stesso livello di disuguaglianza nella distribuzione dei guadagni, almeno secondo quasi tutte le misure abitualmente utilizzate. Fu quel “quasi” a turbare il viaggiatore. Perché la varianza indicava che i redditi erano allocati in modo più diseguale a Zobeide, mentre tutti gli altri indici non segnalavano alcuna differenza? E come mai non vi erano differenze per questi altri indici, nonostante che le loro formule fossero assai diverse? Era necessario proseguire l’indagine.
Il viaggiatore si ricordò di aver letto in gioventù un saggio scritto nel 1920 da Hugh Dalton, un autorevole professore gallese della London School of Economics che gli eventi della vita avrebbero poi portato a diventare Cancelliere dello Scacchiere laburista nel 1945. Dalton sosteneva che la nozione di disuguaglianza non potesse essere scissa dalla visione etica sottostante, poiché altro non è se non la perdita di “benessere sociale” causata da una distribuzione disuguale dei redditi: va quindi misurata con un indice etico, derivato da una specifica funzione matematica che definisce il benessere sociale. Questa visione si contrapponeva nettamente alla tradizione che fino allora aveva proceduto elaborando indici puramente descrittivi, che dessero semplicemente conto della variabilità dei redditi tra gli individui, senza attribuirvi alcun significato normativo. Gini fu pronto a prendere le difese della tradizione, replicando a Dalton che nella misurazione della “… disuguaglianza dei redditi e della ricchezza, indipendentemente da tutte le ipotesi sulla relazione funzionale che le lega al benessere economico, … gli stessi metodi sono … applicabili … a tutte le altre caratteristiche quantitative (economiche, demografiche, anatomiche o fisiologiche)”.
A dispetto della veemente reazione di Gini, al viaggiatore sembrò che l’osservazione di Dalton cogliesse un punto: l’importanza dei giudizi di valore nella misurazione della disuguaglianza. D’altronde, la diversità di opinioni di qualche sera prima tra i suoi amici sembrava esserne una chiara testimonianza. In termini formali, secondo Dalton la funzione di benessere sociale poteva scriversi come somma del benessere di tutti gli individui, cioè come SW=ΣiW(yi) dove W(⋅) dipende solamente del reddito. Il viaggiatore pensò che le cose sarebbero state semplici se W(⋅) fosse stata una funzione lineare. SW sarebbe divenuta una trasformazione lineare del solo reddito medio e un aumento di quest’ultimo sarebbe equivalso a un maggiore benessere complessivo, indipendentemente dalla sua ripartizione – l’ipotesi implicita nei confronti internazionali che si basano esclusivamente sul prodotto interno lordo pro capite. Il viaggiatore calcolò velocemente che il benessere sarebbe risultato maggiore a Zobeide, dove il reddito medio era pari a 114 ducati contro i 76 di Anastasia. Come aveva suggerito il calzolaio. Già, ma che dire del fatto che i redditi erano distribuiti in modo diseguale? Dalton, in effetti, adottava un approccio utilitarista e interpretava W(⋅) come una funzione di utilità (cardinale) identica per tutti gli individui e (strettamente) concava, tale cioè da aumentare meno che proporzionalmente al crescere del reddito. Ne seguiva che la disuguaglianza dei redditi riduceva il benessere della collettività e che questo sarebbe salito ridistribuendo in modo perfettamente ugualitario il reddito totale. Ciò parve ragionevole al viaggiatore, ma quale forma poteva assumere la funzione W(⋅)? Era un dubbio già espresso a pochi anni dalla pubblicazione dell’articolo di Dalton da un economista americano, Dwight Yntema, che aveva osservato come la proposta di questi “si scontrasse con la difficoltà di trovare la funzione che lega il benessere di un individuo al suo reddito come pure con la necessità di ipotizzare che sia identica per tutti gli individui”.
Il viaggiatore trovò la soluzione a questo conundrum – un termine inglese che gli piaceva molto – in un articolo pubblicato mezzo secolo dopo da un altro brillante economista gallese, Anthony Atkinson. Atkinson ebbe l’intuizione di sfruttare alcuni risultati della teoria della scelta in condizioni di incertezza per definire i criteri che una funzione di benessere sociale deve soddisfare per poter ordinare due distribuzioni dei redditi. Quanto più restrittivi sono questi criteri, tanto più è probabile che si possa dire quale sia socialmente preferibile tra le due distribuzioni. Il carattere generale di questi criteri consente di evitare di adottare una specifica funzione W(⋅), ma può tuttavia non essere conclusivo per il confronto, rendendo inevitabile il ricorso a un indice di disuguaglianza, che si basa implicitamente su presupposti ancor più rigidi. Qui interviene la seconda fondamentale intuizione di Atkinson: trasferire l’idea di Dalton dallo spazio delle utilità a quello dei redditi introducendo la nozione di “reddito equivalente a una distribuzione ugualitaria”. Questo reddito y* è quel reddito che se fosse percepito da tutti darebbe un livello di benessere sociale uguale a quello della distribuzione di partenza; è quindi definito implicitamente con l’espressione nW(y*)=ΣiW(yi). Dalla concavità di W(⋅) segue che y* non è superiore a μ, così che il suo scostamento dalla media rappresenta una misura della perdita di benessere sociale causata dalla diseguale distribuzione dei redditi. Si può perciò scrivere un indice etico di disuguaglianza come S=1–y*/μ, che per costruzione è compreso tra 0, quando l’uguaglianza è perfetta, e 1, quando invece è massima. Il valore di y*, e di conseguenza di S, dipende dalla specificazione della funzione W(⋅). Con una funzione isoelastica, W(yi)=yi1–ε/(1–ε) per ε>0 e ε≠1 e W(yi)=ln(yi) per ε=1, si ottiene l’indice suggerito da Atkinson: Aε=1–[Σi(yi/μ)(1–ε)/n]1/(1–ε) per ε>0 e ε≠1 e Aε=1–Πi(yi/μ)(1/n) per ε=1.
L’indice etico così derivato ha una valenza più generale di quella originariamente attribuitagli da Dalton: è sì perfettamente coerente con l’impostazione utilitaristica di quest’ultimo, ma è anche un modo per rendere esplicito, nella scelta della forma funzionale di W(⋅), il giudizio normativo di chi misura il grado di disuguaglianza. In questo secondo caso, la funzione W(⋅) non rappresenta più un’utilità individuale, ma il sistema di ponderazione che il misuratore utilizza per pesare i diversi redditi. Nell’indice Aε, data la forma isoelastica imposta a W(⋅), il parametro ε ne determina la concavità e, conseguentemente, il grado di avversione alla disuguaglianza: più alto è il valore di ε, maggiore è l’attitudine egualitaria del misuratore e il peso che attribuisce alle persone più povere relativamente alle altre; per valori molti elevati di ε, l’indice tende a (1–y1/μ) e dipende, di fatto, solamente dal reddito y1 dell’individuo più povero.
La possibilità di palesare un pluralismo di giudizi di valore non dispiacque al viaggiatore, che si accinse a calcolare l’indice di Atkinson per i guadagni ad Anastasia e a Zobeide. La scelta di ε era un nuovo problema da risolvere, ma una sommaria scorsa agli studi esistenti lo rassicurò che scegliendo valori compresi tra 0,3 e 3 avrebbe coperto un ampio spettro di attitudini alla disuguaglianza. Come atteso, riscontrò che il grado stimato di disuguaglianza aumentava scegliendo un ε più alto, ma ancora una volta non emerse alcuna differenza tra le due città. Un altro punto a favore del contabile.

Rimaneva però al viaggiatore il cruccio dell’anomalia della varianza. Fu allora che si imbatté in un saggio illuminante, pubblicato nel 1976 da un economista francese, Serge Kolm. “Nel maggio del 1968, in Francia, – scriveva Kolm – gli studenti radicali innescarono una protesta che portò i lavoratori a proclamare uno sciopero generale. Tutto finì con l’accordo di Grenelle che riconobbe un aumento del 13 per cento per tutte le retribuzioni. Così, i lavoratori che guadagnavano 80 sterline [sic] al mese ricevettero 10 sterline in più, mentre i dirigenti che già guadagnavano 800 sterline al mese beneficiarono di un aumento di 100 sterline. I Radicali si sentirono amareggiati e truffati; secondo loro, questo accordo aumentava enormemente la disuguaglianza dei redditi … In altri paesi (mi sono stati citati esempi per l’Inghilterra e per i Paesi Bassi), i sindacati dei lavoratori sono più accorti e spesso insistono per aumenti delle remunerazioni uguali in termini assoluti, non relativi, così da evitare l’effetto appena indicato. Ho trovato molte persone che pensano che sia un uguale incremento assoluto di tutti i redditi quello che non accresce la disuguaglianza”. Partendo da questa considerazione, Kolm definì la famiglia di indici assoluti di disuguaglianza Kκ=ln{[Σiexp(κ(μ–yi))]/n}1/κ, dove κ>0 è un parametro che, come ε in precedenza, coglie il grado di avversione alla disuguaglianza. Aumentando κ, si attribuisce più importanza ai redditi più bassi, fino a dar risalto solamente al reddito del più povero con κ molto grande, quando l’indice Kκ tende a coincidere con la differenza (μ–y1). L’indice Kκ non cambia quando tutti i redditi sono aumentati di un pari ammontare, mentre cresce quando sono aumentati in modo proporzionale.
“Ecco dove sta la differenza”, pensò il viaggiatore. “Tutte le misure che ho considerato sino ad ora sono ‘relative’: il loro valore non varia se tutti i redditi sono accresciuti nella stessa proporzione. Fuorché una: la varianza. La varianza rimane immutata solo quando do, o tolgo, a tutti la stessa quantità, proprio come accade per l’indice di Kolm”. Scelse quindi tre valori per κ e calcolò l’indice di Kolm: vide che il livello della disuguaglianza era maggiore per valori più alti di κ in entrambe le città, ma che era senza dubbio superiore a Zobeide che ad Anastasia. Quello che aveva sostenuto il medico!

Mentre calcolava questi ultimi valori, il viaggiatore si rammentò che già Dalton aveva chiaramente distinto tra indici assoluti e relativi. Si rammaricò di non avervi prestato sufficiente attenzione, soprattutto perché l’argomentare di Dalton su quali fossero gli indici da preferire dal punto di vista teorico anticipava l’approccio assiomatico che sarebbe stato seguito nei decenni futuri. Un modo per discriminare tra i diversi indici di disuguaglianza è infatti quello di fissare alcune proprietà “ragionevoli” e scartare quegli indici che non le soddisfano. Annotò le principali di queste proprietà. “Simmetria o anonimità”: l’indice tratta in modo uguale le persone, tralasciando tutte le caratteristiche diverse dal reddito. “Principio della popolazione”: il valore dell’indice non varia quando ciascun individuo nella popolazione è identicamente replicato x volte. “Principio del trasferimento di Pigou-Dalton”: il valore dell’indice diminuisce quando un ammontare di reddito è trasferito da una persona più ricca a una più povera, senza mutarne le posizioni relative, e aumenta nel caso opposto, indipendentemente dai redditi delle altre persone. “Indipendenza rispetto alla scala”: il valore dell’indice non varia quando tutti i redditi sono moltiplicati per la stessa costante positiva. “Scomponibilità”: il valore dell’indice per l’intera popolazione aumenta quando non diminuisce in alcuno dei gruppi ottenuti da una partizione della popolazione e cresce almeno in uno (a parità di dimensione e di reddito medio). Se si segue la proposta di Kolm, l’indipendenza rispetto alla scala è sostituita dalla “indipendenza rispetto a traslazioni”: il valore dell’indice non varia quando lo stesso ammontare è sommato a (sottratto da) tutti i redditi. Di là dalle proprietà che i vari indici soddisfano, la loro diversa sensibilità può essere valutata calcolando come cambiano trasferendo un ammontare di reddito Δ dal più ricco i al più povero j, senza mutarne le posizioni relative. L’indice di Gini varia di [2(j–i)/n2μ]Δ; la deviazione logaritmica media, approssimativamente, di [(yj–yi)/nyjyi]Δ. Poiché per definizione j<i e yj<yi, entrambe le variazioni sono negative, a riprova che i due indici soddisfano il principio di Pigou-Dalton. Un trasferimento progressivo di reddito ha un effetto tanto maggiore sull’indice di Gini, quanto più distanti (nella sequenza ordinata dei redditi) sono le persone coinvolte, indipendentemente dal livello dei loro redditi, una caratteristica che può rendere quest’indice “sgradevole” ad alcuni. Nel caso della deviazione logaritmica media, la diminuzione è invece proporzionale al divario tra i redditi delle due persone.
Il viaggiatore decise che la sua investigazione era giunta alla fine. Gli era ormai chiaro che gli indici di disuguaglianza si distinguono per il peso che implicitamente danno a valori in posizioni diverse della scala dei redditi e che sceglierne uno equivale ad adottare un certo sistema di valutazione delle singole osservazioni e, in ultima analisi, un certo giudizio di valore. Poiché vi è una naturale pluralità di giudizi etici, come la discussione tra i suoi amici gli aveva mostrato chiaramente, in molti casi sarebbe una forzatura sostenere che un indice è migliore di un altro. Fu confortato in questa sua conclusione dallo scoprire che vi è un consenso tutt’altro che unanime intorno alla plausibilità delle proprietà degli indici di disuguaglianza che si era annotato. Era questo, infatti, il verdetto delle verifiche sperimentali compiute sottoponendo quesiti verbali e numerici a vari gruppi di studenti universitari in Europa, Oceania, Israele e Stati Uniti.
Si convinse che la misurazione della disuguaglianza è un processo complesso, che può fornire risultati differenti, talora anche contrastanti, a seconda delle soluzioni adottate. Questa pluralità di risultati non è però un sintomo di inadeguatezza della teoria, ma è la conseguenza della complessità costitutiva della nozione di disuguaglianza, in cui convivono una natura “descrittiva” – la condizione fattuale di diversità tra soggetti – e una “normativa” – il giudizio di equità della distribuzione rispetto a un qualche termine di riferimento ideale. Come ha scritto il grande economista indiano Amartya Sen, “... una misura può difficilmente essere più precisa della nozione che rappresenta”.
Compiaciuto dei suoi progressi, il viaggiatore decise di invitare nuovamente a cena il contabile, il medico e il calzolaio per illustrargli i risultati delle sue ricerche e rassicurarli che tutti e tre avevano colto un aspetto importante del confronto tra i guadagni ad Anastasia e quelli a Zobeide.
Pubblicato in “Matematica e democrazia”, a cura di A. Guerraggio, PRISTEM/Storia - Note di Matematica, Storia e Cultura, n. 39-40, pp. 171-182, Milano, Egea, 2015. Con molte scuse a Italo Calvino, per l’uso improprio delle sue città invisibili.







