Prendere le misure e calcolare i rapporti / La nuova didattica: muoversi verso un'idea
A0, A1, A2, A3, A4, A5, A6, A7, A8, A9, A10. Sono i formati dei fogli sui quali scriviamo e disegniamo. Tagliando a metà un formato nel senso della larghezza si ottiene quello successivo, in modo tale che il rapporto tra il lato maggiore e il lato minore del primo sia uguale al rapporto tra lato maggiore e il lato minore del secondo. In termini matematici, se consideriamo “a” il lato maggiore e “b” quello minore, si ottiene la proporzione: a:b = b:a/2. La gabbia o griglia compositiva usata per impaginare gli elementi grafici e/o testuali su un foglio da disegno come su una pagina tipografica discende da questa proporzione, che si può tradire ma non ignorare.
Tra il 29 novembre 2012 e il 13 gennaio 2013 fu allestita a Milano (Palazzo Reale) la mostra Giulio Einaudi. L’arte di pubblicare dedicata alla collana I Coralli. La mostra si focalizzava sul legame tra Giulio Einaudi e le arti visive. Tra i materiali esposti si potevano ammirare i nove Coralli della Serie Bianca progettati dall’artista Giulio Paolini e stampati tra il 1976 e il 1978. I volumi non erano rifilati e perciò il lettore doveva tagliare le pagine con un tagliacarte ottenendo un contrasto tra il ruvido-sfrangiato del taglio delle pagine (davanti, testa e piede) e la copertina liscia e lucida.La prima versione deI Coralli fu stampata su formato cartaceo 130x195 mm nella proporzione 2:3 diapente e impaginata secondo uno schema derivato dal “Canone segreto” impiegato nei manoscritti tardo medioevali: due angoli dell’area di testo giacciono sulle diagonali della doppia pagina e un terzo angolo sulla diagonale della pagina singola, in modo tale che le aree di testo abbiano le stesse proporzioni delle pagine del libro. La quarta e ultima versione de I Coralli fu stampata nel formato 120x192 mm con un rapporto 5:8. Sono queste le proporzioni dei nove progettati da Paolini. Sovrapponendoli si ottiene un parallelepipedo che trasporta le proporzioni grafiche nella terza dimensione della scultura. Il parallelepipedo può infatti essere considerato una scultura minimalista o anche un’istallazione.
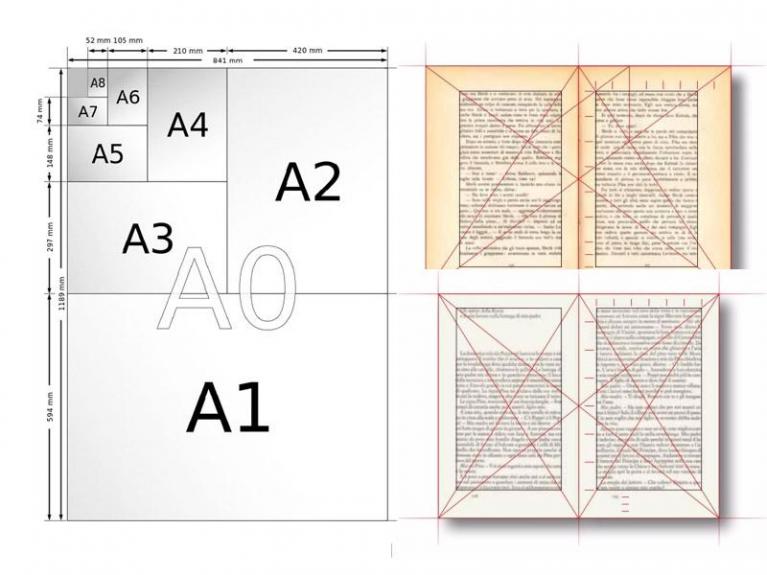
A sinistra i formati della serie A; a destra e in alto le proporzioni della prima versione de I Coralli; a destra e in basso le proporzioni della quarta versione.
Nell’opera di Giulio Paolini, così come nella didattica del comporre sulla superficie di un foglio, la proporzione del formato dalla quale discende la modularità e la simmetria della griglia compositiva (il termine “simmetria” è qui inteso nell’accezione antica, greca e poi latina, come rispondenza di proporzioni tra le singole parti e l’intera figura) fornisce il contesto metrico nel quale si sviluppano le relazioni tra i diversi elementi ivi inseriti. Modificando la posizione, l’orientamento, la grandezza delle immagini o dei blocchi di testo in base alle necessità del comporre possiamo ristrutturare il senso di ciò che vediamo e leggiamo. In altri termini, l’accordo metrico e quindi proporzionale tra gli elementi grafici e/o testuali inseriti nella griglia compositiva orienta il senso della loro lettura e interpretazione, insieme a vari fattori percettivi e all’ordine crono-logico della scrittura alfabetica che lo compenetra. La logica lineare della riga s’innesta così in quella metrica del comporre.

Dettaglio della mostra "Giulio Einaudi. L'arte di pubblicare".
In conclusione, sulla superficie di un foglio, sia esso quello delle diverse versioni de I Coralli o quello della tavola grafica nel formato B2 500×707 millimetri (la serie B dei formati è definita in rapporto alla serie A) sulla quale lo studente di una scuola d’arte sviluppa le sue idee, scrittura e arti visive dialogano tra loro usando il linguaggio matematico della proporzione, per dar luogo a strategia di pensiero che è insieme anche visione.
Sono questioni di una certa rilevanza per l’istruzione artistica italiana alle prese con il problema del rapporto tra discipline artistiche, umanistiche e scientifiche. La rete scolastica Progetto Licei Artistici 2016/2017 ha promosso un confronto tra docenti articolato in nove incontri (dal 03 marzo al 19 maggio 2017) per mettere a punto una proposta di curriculo delle discipline d’indirizzo artistico omogeneo a livello nazionale.
Nel corso dei lavori svolti dalla commissione di studio Arti Figurative si è discusso anche sul fatto che una didattica pluridisciplinare basata sui processi percettivi e cognitivi messi in atto dallo studente nel corso del processo di apprendimento può avere più successo di una didattica basata sui“prodotti”. Le UdA (Unità di Apprendimento) pluridisciplinari, che costituiscono lo strumento didattico privilegiato della recente riforma scolastica, sono focalizzate sulla realizzazione di un prodotto o compito di realtà da portare a termine in un determinato contesto operativo. Si è notato che portando l’attenzione dello studente sul processo che conduce alla realizzazione del prodotto, piuttosto che sulla realizzazione del prodotto stesso, si stimola un approccio critico altrimenti inibito dalle esigenze procedurali del compito.

Tavolo di lavoro di uno studente.
A questo riguardo sono stati portati ad esempio dei percorsi didattici effettuati nel corso del corrente anno scolastico, tra i quali dei metodi impiegati dagli studenti per la ricerca delle idee in una fase della progettazione. Uno di questi consiste nell’impiegare la griglia compositiva come ordine e misura delle associazioni visive e semantiche generate dallo studente mentre si muove con il pensiero alla ricerca di un’idea. Nella griglia compositiva gli elementi grafici e testuali si combinano tra loro sulla base di una rispondenza di proporzioni tra le singole parti e l’intera figura e, al tempo stesso, secondo la necessità crono-logica del raccontare e del ragionare. L’idea si evolve dalla fase di schizzi, che ha carattere narrativo, alla successiva fase di studi dove il narrare trascorre progressivamente in un ragionamento che ha i caratteri di quello ipotetico. Nella metrica del comporre fluisce quindi crono-logicamente anche una narrazione e procede un ragionamento.
Guidata dalla griglia compositiva, la fase narrativa degli schizzi è caratterizzata da una concatenazione analogica di immagini, parole e concetti. Proporzione e analogia si trovano qui strettamente allacciate tra loro. Il termine “analogia”, dal greco antico “ἀναλογία”, è dotato di due significati. Il primo è riferito ai nessi e alle similitudini che possiamo scorgere tra cose, situazioni ed eventi diversi tra loro; il secondo richiama la sua origine matematica, ossia il rapporto che lega i termini in una proporzione.
L’analogia è una strategia di pensiero dotata di un’intrinseca razionalità. Secondo alcuni studi neo-piagetiani di psicologia applicata sembra anche avere effetti positivi sull’abilità di ragionare e quindi sulla formazione delle strutture logiche. Analogia e logica sono due strategie di pensiero complementari e ugualmente razionali se pur fondate su principi diversi.

Nel suo libro La linea e il circolo. Studio logico-filosofico sull’analogia (Quodlibet, 2004) considerato da Giorgio Agamben uno dei più importanti saggi della filosofia del Novecento, Enzo Melandri porta l'attenzione sull'analogia come forma di conoscenza razionale. Il filosofo sostiene che lo sviluppo del pensiero matematico è stato compromesso dal fatto che il logos della proporzione ha dovuto soccombere a quello della dialettica, che “la matematica è stata sacrificata alla logica”. Secondo Melandri l’analogia è un aspetto della razionalità complementare alla logica: “L’analogia [scrive l’autore] ha le sue proprie tautologie che, pur essendo come tali altrettanto razionali che quelle in senso stretto logiche, possono tuttavia costituirsi in sistemi alternativi rispetto a queste ultime”. “Alternativi” nel senso che uno è complementare rispetto all’altro, non che lo sostituisce.
Nello stesso saggio Melandri cita anche Ernst Hermann Hänssler a proposito di una sua tesi, secondo la quale la struttura dell’analogia è originariamente connessa a quella di simmetria.
Inoltre, se gli schemi percettivi sono regolati dagli stessi principi della fisica e della biologia come sostenuto da Wolfgang Köhler con la teoria dell’isomorfismo (La Psicologia della Gestalt, Feltrinelli, 1961) possiamo considerare la simmetria di Hänssler (riferita anche all’anatomia e alla fisiologia della mente umana) non solo connessa all’analogia ma anche ai meccanismi della percezione visiva. Gli studi condotti da Rudolf Arnheim (Il pensiero visivo. La percezione visiva come attività conoscitiva, Einaudi, 1974) hanno messo in luce come la percezione visiva possa costituire in sé una forma di pensiero e per quanto riguarda la simmetria nella quale l’analogia affonda le sue radici, la principale legge della Psicologia della Gestalt detta della pregnanza si basa appunto sui principi di simmetria ed equilibrio.
Riassumendo: scrittura e arti visive dialogano tra loro sulla superficie di una pagina o di un foglio usando il linguaggio matematico della proporzione e quindi della simmetria, secondo Hänssler, Melandri e altri studiosi, forma originaria dell’analogia.

Studenti impegnati nella copia della Venere di Cirene, calco in gesso tratto dall'originale del IV secolo a.C. conservato presso il Museo Archeologico di Tripoli.
Alla luce di quanto si è detto, tornando alle riflessioni sulla metrica del comporre che sviluppa competenze trasversali oltre che d’indirizzo, è auspicabile che lo scambio tra l’area artistica, umanistica e scientifica nella didattica dei licei artistici italiani non si concretizzi in un collage di discipline incollate tra loro da un prodotto, ma in un’esplorazione critica dei processi percettivi e insieme cognitivi messi in atto dallo studente nel suo muoversi verso un’idea. Tutto ciò allo scopo di favorire lo sviluppo delle competenze trasversali o soft skills richieste dal nuovo sistema d’istruzione e dal mondo del lavoro, tra le quali quella logico-matematica, il problem solving, l’approccio critico, la creatività e la flessibilità mentale, alle quali è indispensabile aggiungere anche quella di cogliere il rapporto tra le singole parti e l’intera figura, la capacità di cogliere una simmetria innestando così la razionalità metrica in quella logica.
L’iconografia popolare dell’artista con il braccio teso in avanti mentre ritrae il modello vivente o la copia in gesso di una scultura antica racchiude l’archetipo di questa razionalità metrica. Così facendo l’artista prende le misure e calcola rapporti, che poi trascrive secondo proporzione su un foglio di carta da spolvero o su un piano di creta.